Shunting Yard, Javascript
Shunting Yard (Part 1)
The Shunting Yard Algorithm is, quite possibly, my favorite algorithm. It transforms a series of tokens into an abstract syntax tree, taking into account operator type, precedence, and parenthesis.
Through the next series of articles, I want to build a general purpose expression parser using the algorithm. By the end, we’ll have an algorithm that can be easily extended to add many different types of operators… any arity (unary, binary, ternary, etc), prefix, infix, and postfix.
Series: Part 1, Part 2, Part 3…
The Problem
First: what is the problem we’re trying to solve?
We’ll save lexical analysis for another article. For now, let’s assume we have a series of tokens. For example:
// tokens for the input string: "3 + 7 * -10"
var tokens = [
{ type: 'num', value: 3 }, // the number 3
{ type: 'sym', value: '+' }, // the symbol '+'
{ type: 'num', value: 7 }, // the number 7
{ type: 'sym', value: '*' }, // the symbol '*'
{ type: 'sym', value: '-' }, // the symbol '-'
{ type: 'num', value: 10 } // the number 10
];
Remember: the lexer is very dumb. It is simply scanning the input string from left to right,
saying, “I see the number 3… I see the + symbol… I see the number 7… I see the *
symbol…”
We need to convert this into an abstract sytax tree (AST), like this:
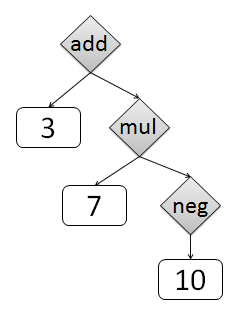
Abstract syntax tree of: 3 + 7 * -10
Which we’ll represent in JavaScript as:
var ast = {
type: 'add', // the addition operator
parms: [{
type: 'val', // the value 3
value: 3
}, {
type: 'mul', // the multiplication operator
parms: [{
type: 'val', // the value 7
value: 7
}, {
type: 'neg', // the negation operator
parms: [{
type: 'val', // the value 10
value: 10
}
]
}
]
}
]
};
The idea can be represented in code many different ways, but the core is the same: each node in the AST is either a terminal or a non-terminal.
A terminal is something that terminates the tree – it is a leaf node. In our example, 3, 7,
and 10 are all terminals. They don’t have any children nodes. These are represented in our AST
as objects with type set to 'val'.
Non-terminals are things that contain more nodes. In the example, add, mul, and neg are
non-terminals. They operate on their parameters and produce a value that is passed up along the
tree.
Shunting Yard Skeleton
Where to even start? First, let’s build the most basic Shunting Yard function, so we can inspect it fully:
function SimpleShuntingYard(tokens){
// helper function to get next token and validate its type
var tokenIndex = 0;
function NextToken(requiredType){
if (tokenIndex >= tokens.length)
throw 'invalid expression: missing token';
var tok = tokens[tokenIndex];
tokenIndex++;
if (tok.type != requiredType)
throw 'invalid expression: expecting ' + requiredType;
return tok;
}
// helper function to apply binary op based on a symbol
function ApplyBinOp(symbol, left, right){
var sym_to_type = {
'+': 'add',
'-': 'sub',
'*': 'mul',
'/': 'div'
};
if (!sym_to_type[symbol])
throw 'invalid expression: unknown operator ' + symbol;
return {
type: sym_to_type[symbol],
parms: [left, right]
};
}
var tok, nextValue;
var lastOp = false;
var lastValue;
function ApplyLastOp(){
// if we don't have a prev operator, then use the terminal
if (lastOp === false)
lastValue = nextValue;
else // otherwise, we have a pending operator, so apply it
lastValue = ApplyBinOp(lastOp, lastValue, nextValue);
}
while (1){
// grab a terminal (which is always type 'num', for now)
tok = NextToken('num');
// create the terminal node
nextValue = {
type: 'val',
value: tok.value
};
// if we're out of tokens, then exit
if (tokenIndex >= tokens.length)
break;
// otherwise, we must have a binary operator
// grab an operator (which is always type 'sym', for now)
tok = NextToken('sym');
// apply any shunted operators
ApplyLastOp();
// save the new operator to be applied later
lastOp = tok.value;
}
// apply any remaining shunted operators
ApplyLastOp();
// all done, so return the top of the tree
return lastValue;
}
What the hell is even going on in this piece of code! Does it actually work?
This may seem like a lot, but removing error checking, comments, and blank lines, the core algorithm is about 50 lines.
This simple algorithm can build ASTs for some expressions… but not all. Here are the results
for the expression 2 * 3 + 4:
var tokens = [
{ type: 'num', value: 2 },
{ type: 'sym', value: '*' },
{ type: 'num', value: 3 },
{ type: 'sym', value: '+' },
{ type: 'num', value: 4 }
];
SimpleShuntingYard(tokens);
=> {
type: 'add',
parms: [{
type: 'mul',
parms: [{
type: 'val',
value: 2
}, {
type: 'val',
value: 3
}]
}, {
type: 'val',
value: 4
}
]
}
Hey, that’s right..! How did it do that?! Let’s start by inspecting the easier parts, then building up (HAHA! get it? …no? ;-P).
NextToken
The NextToken function is responsible for getting the next token and validating it against the
required type:
var tokenIndex = 0;
function NextToken(requiredType){
if (tokenIndex >= tokens.length)
throw 'invalid expression: missing token';
var tok = tokens[tokenIndex];
tokenIndex++;
if (tok.type != requiredType)
throw 'invalid expression: expecting ' + requiredType;
return tok;
}
Notice that tokenIndex starts at 0, and continues counting up as tokens are requested. If
there aren’t any more tokens, or if the token is the wrong type, then errors are thrown. Otherwise,
the function simply returns the next token.
ApplyBinOp
The ApplyBinOp is also fairly straight forward:
function ApplyBinOp(symbol, left, right){
var sym_to_type = {
'+': 'add',
'-': 'sub',
'*': 'mul',
'/': 'div'
};
if (!sym_to_type[symbol])
throw 'invalid expression: unknown operator ' + symbol;
return {
type: sym_to_type[symbol],
parms: [left, right]
};
}
Given a symbol, left node, and right node, we need to construct a binary operator node. This is
simple. First, have a map between symbols and binary operators. If the given symbol isn’t in the
map, then the user has provided an invalid operator. Otherwise, return the node object, with
type set to the operator, and parms set to a list containing the left and right nodes.
Easy. Now for the meat:
The Shunt
Next, let’s look at the lastOp variable. This is the most important variable – it is the spirit
of the Shunting Yard algorithm.
The Shunting Yard algorithm works by postponing application of operators. Why do we need to postpone? Because we haven’t gathered all the parameters yet!
We are scanning the tokens, from left to right. When we hit a binary operator, we need to wait before creating the node, because we don’t have all the information just yet. We need to grab the next terminal before we can create the node.
Once we grab the next terminal, we are free to create the node. That’s what this line does:
lastValue = ApplyBinOp(lastOp, lastValue, nextValue);
Remember: nextValue is always the terminal we just grabbed:
// create the terminal node
nextValue = {
type: 'val',
value: tok.value
};
And lastOp contains the symbol we collected right before looping around:
// save the new operator to be applied later
lastOp = tok.value;
So: what is lastValue doing in there?
The Tree
The lastValue variable is the magic that builds the AST. Before we can understand what it’s
doing, we need to widen our inspection:
function ApplyLastOp(){
// if we don't have a prev operator, then use the terminal
if (lastOp === false)
lastValue = nextValue;
else // otherwise, we have a pending operator, so apply it
lastValue = ApplyBinOp(lastOp, lastValue, nextValue);
}
When we go through the loop the first time, we don’t have a lastOp – we indicate this by
initializing lastOp to false. Therefore, the first time through the loop, lastValue is
simply set to nextValue, which is the terminal.
But the second time around, lastOp contains a symbol and lastValue will contain the previous
terminal. We will load the next terminal into nextValue. It’s at this point we execute:
lastValue = ApplyBinOp(lastOp, lastValue, nextValue);
What happens? The binary operator node is created, with the previous operator, the previous value,
and the terminal we just read. Great – but why assign the results to lastValue?
We assign the resulting node to lastValue so that when the loop goes around a third time,
lastValue will contain the binary operator (which, in turn, contains the terminals). This is
what builds our tree. We are moving from terminals (leaf nodes), upwards along the branches,
building larger and larger trees, using the binary operator nodes to collect everything.
In fact, once you understand these two concepts (lastOp for postponing operator application, and
lastValue for tree building), you understand the core of the Shunting Yard algorithm.
Bad News
I’m sorry to break it to you, but our skeleton has some glaring holes. It doesn’t work with unary operators, ternary operators, postfix operators, parenthesis, and it has no concept of operator precedence.
Don’t worry! In follow-up articles, we’ll patch those holes. For now, make sure you completely understand how and why the current algorithm works (for certain expressions). This is the foundation upon which we’ll add all the other features… but those features won’t make sense unless you understand the foundation.